The Long and Short of Kurtosis
Michael J. Cleary, Ph.D.
mcleary@qualitydigest.com
Story update 9/17/2018: The formula for kurtosis was missing "n" in the denominator. That has been fixed.
Hartford Simsack’s failed
attempt to harness the power of p-charts in his quest for
the elusive Black Belt hasn’t daunted him. Premature
boasting about his accomplishments—and then falling
short—has renewed his determination to save Greer
Grate & Gate enough money so that he’ll receive
the acknowledgment he so richly deserves for his demonstrated
statistical prowess. In the meantime, his son, who achieved
black belt status at age 11, has given up his martial arts
and gone back to watching cartoons and eating jelly doughnuts.
Line five in Simsack’s plant, which assembles wrought-iron
fencing for interior use, had 421 defects last month, each
of which cost GG&G $150.22. Although Simsack had originally
aimed for savings in the millions, his sights have come
down slightly, and a savings of $63,242.62 that could be
realized from this process piques his interest. Besides,
he thinks he has the answer that will, in fact, generate
these cost savings.
Simsack takes unprecedented action: He discusses the defect
with the line process operator, who has a fairly clear idea
about the defect’s source. Simsack sees an immediate
opportunity to take credit for fixing something. With his
reputation for genius, who would doubt that it was his own
idea?
Armed with a histogram showing that, with a Cpk of 1.0,
the process is barely capable, he mentions to his boss Rock
deBote what a great job he’s done using the power
of statistics to single-handedly improve the company. As
he spreads out the histogram, deBote notices other statistics
relating to the process, including a kurtosis of -0.62.
Noticing his boss staring intently at the kurtosis figure,
Simsack attempts to pass over the number’s meaning
because he has no idea what significance it holds. “Of
course the kurtosis is negative,” he says, shaking
his head in dismay, “but my plan is to improve that
by 100 percent.” Does this make sense in the ongoing
improvement of the process?
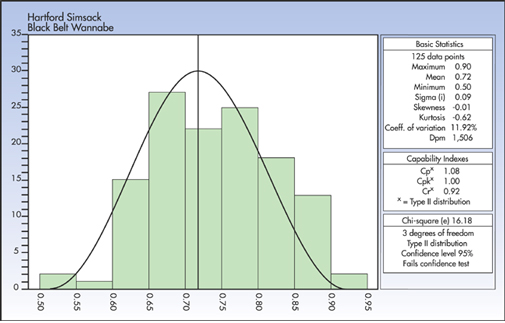
No, it doesn’t make sense.
As anyone who hasn’t fallen asleep in statistics class knows, kurtosis is a measure of the combined weight of the tails relative to the rest of the distribution. Sometimes it’s referred to as the
“fourth movement.” The formula for kurtosis
is:
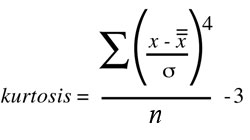
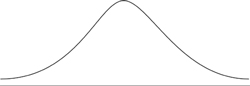
A normal distribution has a kurtosis of zero and is known
as “mesokurtic.”
On the other hand, if a distribution is tighter and taller
than a normal distribution, the kurtosis would be a positive
number. This distribution is referred to as “leptokurtic”
because it has a long tail like a kangaroo.

Finally, for a distribution that is flatter than a normal
curve, the kurtosis would be negative, or “platykurtic”
with a short tail—like a platypus.

If you want to hurl a sophisticated invective at a co-worker,
accuse him or her of platykurtic (i.e., non-normal) tendencies.
Michael J. Cleary, Ph.D., founder and president of
PQ Systems Inc., is a noted authority in the field of quality
management and a professor emeritus of management science
at Wright State University in Dayton, Ohio. A 29-year professorship
in management science has enabled Cleary to conduct extensive
research and garner valuable experience in expanding quality
management methods. He’s published articles on quality
management and statistical process control in a variety
of academic and professional journals. Note: Kangaroo and
platypus drawings are adapted from similar drawings in Donald
L. Harnett’s, Statistical Methods, Third
Edition (Addison-Wesley Publishing Co., 1982).
Letters to the editor regarding this column can be
sent to letters@qualitydigest.com.
|