Building an
Acceptance Chart
by Donald S. Holmes and A. Erhan Mergen
These handy tools can help you meet specification limits. There are some processes that, due to their nature, are expected to have unavoidable shifts in their average value but which are still able to
satisfy customer-established specifications. This situation occurs when the standard deviation of the process at the various average values of the process is very small relative to the tolerance
width, that is, the difference between the upper and lower specification limits. In usual statistical process control terms, such a process is not in control but may be able to produce acceptable
product. As you read statistical literature, it will appear that three different kinds of charts are being generated for the aforementioned situation. This is incorrect; there
is actually only one type: a chart using sample averages that allows you to detect when processes will produce an unacceptable level of nonconforming products. The literature's references to
"acceptance control charts" should really be changed to "acceptance charts" because these charts deal only with the issue of whether the process should be accepted or rejected. There are really
two different issues: acceptance and control. These two issues are independent of each other. Acceptance
Acceptance deals with the ability of a process to meet specifications. Control deals with the ability of a process to perform in a consistent, stable fashion.
There are three design approaches you can use for building acceptable quality level (AQL) acceptance charts: designs based on rejectable quality level (RQL) and beta risk; designs based on
AQL and alpha risk; and designs based on RQL, AQL, beta and alpha. Some writers refer to the chart generated with an AQL-based design as a modified control chart, and others simply call it an
acceptance control chart. Authors in general seem to agree that charts using RQL or a combination of RQL and AQL to establish risk levels should use the word "acceptance" in their titles. We
suggest that the word "control" be eliminated because the charts are used simply for acceptance purposes.
How to build an AQL acceptance chart Here's how an AQL acceptance chart is constructed for subgroup sample averages using the upper specification limit (USL) case to
demonstrate the principle. [The lower specification limit (LSL) case is done in essentially the same fashion.] Step 1. Decide on the AQL appropriate for the process. Step 2. Set a value known as the upper acceptable process mean (UAPM) at k1sx below the USL, where sx is the capability standard deviation of the x's. If the x values are roughly normally distributed, then using k1
= 2 will produce an AQL value of approximately 2.5% (see Figure 1). Figure 1: Graphical Display of UAPM
Step 3. Add k2s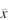 to UAPM to arrive at the upper acceptance limit (UAL) for the sample to UAPM to arrive at the upper acceptance limit (UAL) for the sample 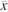 , where s , where s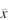 is the standard deviation of the
is the standard deviation of the 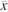 's. The value of k2 sets
the probability of acceptance of material that has a quality level of AQL. Choosing k2 = 2 would set the probability of accepting material that has a
quality level of AQL to approximately 0.975 (see Figure 2). 's. The value of k2 sets
the probability of acceptance of material that has a quality level of AQL. Choosing k2 = 2 would set the probability of accepting material that has a
quality level of AQL to approximately 0.975 (see Figure 2). Figure 2: Graphical Display of UAL
Remember that the standard deviation of the 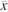 's is the standard deviation of the x's divided by the square root of the sample size, i.e., where n is the sample size. 's is the standard deviation of the x's divided by the square root of the sample size, i.e., where n is the sample size. 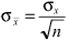 Equations UAL for 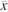 's for an AQL acceptance chart is calculated as follows: 's for an AQL acceptance chart is calculated as follows:
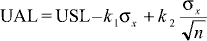
Lower acceptance limit (LAL) for 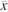 's for an AQL acceptance chart is calculated as: 's for an AQL acceptance chart is calculated as: 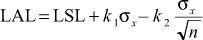
where LSL is the lower specification limit. Example Suppose we have a process whose output is approximately normally
distributed. Engineering tolerances (i.e., specification limits) are 50 ± 10. The process has a capability standard deviation of 1--about 1/20th of the
tolerance--so acceptance charts are a viable alternative. The primary interest is to supply material that meets specifications (not necessarily "in control"). A
sample size of 9 will be used to calculate 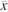 's. 's.
To construct the chart, the following steps are taken: Step 1. If an AQL value of 2.5% is desired, then k1 is 2. Step 2
. The UAPM is then 60 – 2(1) = 58 Step 3. If the probability of acceptance is set at 0.975, then k2 would be 2 and the UAL for sample 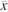 for sample size 9 is then for sample size 9 is then 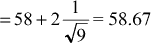 Now reverse this procedure to find the lower acceptable process mean
(LAPM) by taking LSL and adding 2 times the standard deviation of 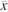 '
s. In this case it would be '
s. In this case it would be LAPM = 40 + 2(1) = 42 From this value, subtract 2 times standard deviation of 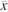 to get the lower acceptance limit (LAL) for the sample averages, which would be to get the lower acceptance limit (LAL) for the sample averages, which would be 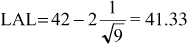 We use the chart as follows: Take a sample of size 9 and calculate the average (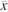 ). If ). If 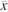 is less than 58.67 and is greater than 41.33, then accept the process. Otherwise reject the process as one that is generating a 2.5% (or worse) quality level. is less than 58.67 and is greater than 41.33, then accept the process. Otherwise reject the process as one that is generating a 2.5% (or worse) quality level. Why use an acceptance chart?
Given that the process standard deviation is small compared to tolerance, width acceptance charts are good alternatives to process control charts if the primary
objective is to meet the specification limits rather than monitor process stability. This knowledge is timely in that many companies have high-tech processes with
small standard deviations for which acceptance charts would be valuable tools. References
1. Duncan, A.J., Quality Control and Industrial Statistics, fifth edition. Illinois: Irwin, 536–540, 1986. 2. Freund, R.A., "Acceptance Control Charts,"
Industrial Quality Control, Vol. 14, No. 4, 13–23, October 1957. 3. Holmes, D.S., and A.E. Mergen, "Process Acceptance Charts for Short Runs," Quality Engineering,
Vol. 10, No. 1, 149–153 1997. 4. Holmes, D.S., and A.E. Mergen, "EWMA Acceptance Charts," Quality and Reliability Engineering, International, Vol. 16, No. 2, 1–4, 2000. 5. Montgomery, D.C., Introduction to Statistical Quality Control, third edition New York: John Wiley and Sons, 354–358, 1996. About the authors Donald S. Holmes is president of Stochos Inc. of Schenectady, New York.
He is a retired professor of the Graduate Management Institute at Union College in Schenectady. Holmes, a CQE, has master's and bachelor's
degrees in mathematics and is a Fellow of the American Society for Quality. E-mail him at dholmes@qualitydigest.com .
A. Erhan Mergen is the dean's research professor in quality, decision sciences, College of Business at the Rochester Institute of Technology in
Rochester, New York. He has a doctorate in administrative and engineering systems, a master's degree in industrial administration and a
bachelor's degree in management. Mergen is a member of the American Society for Quality. E-mail him at amergen@qualitydigest.com . |