Ever since he assumed the position of quality manager for Greer Grate & Gate, Hartford Simsack has become a
self-avowed statistical expert. Pondering how he can broaden his reputation within the organization, Simsack considers strategies that will call attention to his expertise.
Simsack reflects on his mentor, Dr. Stan Deviation, who is respected for his knowledge and has gained a venerable position on the college faculty. "How has he done that?" Simsack wonders.
He comes to the conclusion that one way to assume a higher profile is by doing exactly that: Deviation is, after all, the only one standing up during his classroom lectures, while everyone else
is sitting down, taking notes. "I need to figure out a way to be the one standing up," Simsack concludes. With renewed confidence in his ability to get ahead, Simsack plans a
course on understanding X-bar and R charts for quality technicians at Greer Grate & Gate. This audience will witness his brilliance firsthand, he assures himself, and his boss will learn
about it as well. Not wanting to invest too much effort, however, Simsack borrows Deviation's copy of Total Quality Tools and copies the chapter concerning chart
interpretation. This will provide course materials, he thinks, and no one knows or cares about copyright infringement. Because Deviation believes in beginning with manual charts to gain an
understanding of the charting process prior to relying on software to do the hard part, Simsack plans to walk his students through an exercise--also taken from the book. The
example presents 20 samples of the size 5. When his boss enters the classroom to observe, Simsack is demonstrating how to calculate the upper control limit, using the following formula:
Although Simsack's confidence is buoyed by his reliance on Total Quality Tools, he isn't prepared when a student asks, "What does the A2 mean?"
Simsack replies with an unintelligible mumble, his typical response when he becomes nervous. After studying the following table, another student asks why
A2 becomes smaller as the sample size becomes larger.
"Well, larger sample sizes are simply more complete," Simsack stammers. But why does A2 really become smaller as n gets larger?
a) Simsack is correct. This is what's meant by "robust sampling." b) As the sample size enlarges, R-bar can only become smaller, by definition.
c) The LaGrangian multiplier causes numbers to become smaller. d) One would expect that the larger the sample, the greater the R-bar would be, so A2 must compensate for this. Answer d is correct. We recall that Walter A. Shewhart's theory requires
control limits three standard errors above the process average and three standard errors below it. (Note: People will sometimes express this as "three
standard deviations," but the correct language is "three standard errors.") Statisticians' ability to calculate a standard deviation during the 1930s was more
limited (Do you recall mechanical calculators?), so Shewhart needed a way to estimate it. The standard error is sigma divided by the square root of the sample size (n). 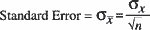
By multiplying A2 by R-bar, one estimates three standard errors. As the sample size becomes larger, one would expect the range to be larger. For example, when considering an X-bar and R chart of a process with samples
of two each time, one would expect the range to be smaller than if samples of 10 had been used. If A2 times R-bar represents an estimation of three standard errors, then A2
must become smaller as n becomes larger, in order to compensate for the fact that larger sample sizes will produce larger R-bars.
Simsack, if he wants to enhance his wisdom about statistics, might consider getting to the "whys" of his memorized formulas. About the author Michael J. Cleary, Ph.D., is a professor emeritus at Wright State
University and founder of PQ Systems Inc. He has published articles on quality management and statistical process control in a variety of academic and professional journals.
E-mail Cleary at mcleary@qualitydigest.com . Letters to the editor regarding this column can be e-mailed to letters@qualitydigest.com . |