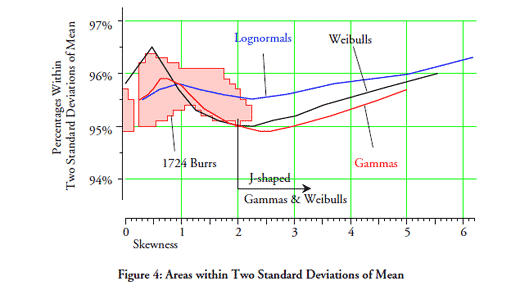
Last month we looked at what the empirical rule tells us about the data in a histogram. This month we will consider if there are any commonalities between different probability models that will allow us to make categorical statements without having to know the exact form of the probability model.

In order to work with multiple probability models we will need some systematic way to organize them relative to each other. We will need this organization in order to have a context for any generalizations we may make about probability models. The organizational device we shall use is the traditional one created by Karl Pearson more than 100 years ago—the shape characterization plane.

The shape characterization plane

Instead of trying to organize drawings of many different probability density functions, Karl Pearson decided to use a more mathematical approach. He would organize collections of probability models using the “shape parameters” of skewness and kurtosis. By plotting these two parameter values as points in a plane he could show similarities and differences between distributions.

The skewness parameter for a probability model with density function f(x) is traditionally defined as:

 …