Anticipating challenges is always a daunting task for continuous improvement professionals. Unforeseen inefficiencies in process or defects in product development can throw timelines and associated costs into disarray. How to commit to realistic forecasts and timelines when resources are limited, or gathering real data is too expensive or impractical? Can simulated data be trusted for accurate predictions? That’s when Monte Carlo simulation comes in.

Simulated data actually are routinely used in situations where resources are limited, or gathering real data would be too expensive or impractical, though. Monte Carlo simulation is a mathematical modeling technique that allows you to see all possible outcomes and assess risk to make data-driven decisions. Historical data are run through a large number of random computerized simulations that project the probable outcomes of future projects under similar circumstances.

The Monte Carlo method uses repeated random sampling to generate simulated data to use with a mathematical model. This model often comes from a statistical analysis, such as a designed experiment or a regression analysis.

Suppose you study a process and use statistics to model it like this:

With this type of linear model, you can enter the process input values into the equation and predict the process output. However, in the real world, the input values won’t be a single value, thanks to variability.

Unfortunately, this input variability causes variability and defects in the output.

Design a better process while taking uncertainty into account

To design a better process, you could collect a mountain of data to determine how input variability relates to output variability under a variety of conditions. However, if you understand the typical distribution of the input values and you have an equation that models the process, you can easily generate a vast amount of simulated input values and enter them into the process equation to produce a simulated distribution of the process outputs.

You can also easily change these input distributions to answer “what if” types of questions. That’s what Monte Carlo simulation is all about. In the example we are about to work through using Companion by Minitab, we’ll change both the mean and standard deviation of the simulated data to improve the quality of a product.

Step-by-step example of Monte Carlo simulation using Companion by Minitab

A materials engineer for a building products manufacturer is developing a new insulation product.

The engineer performed an experiment and used statistics to analyze process factors that could affect the insulating effectiveness of the product. For this Monte Carlo simulation example, we’ll use the regression equation shown above, which describes the statistically significant factors involved in the process.

Step 1: Define the process inputs and outputs

The first thing we need to do is to define the inputs and the distribution of their values.

The process inputs are listed in the regression output, and the engineer is familiar with the typical mean and standard deviation of each variable. For the output, she can copy and paste the regression equation that describes the process from Minitab Statistical Software into Companion’s Monte Carlo tool.

It’s an easy matter to enter the information about the inputs and outputs for the process as shown:

Click here for larger image.

Verify your model and then you can run a simulation (Companion quickly runs 50,000 simulations by default, but you can specify a higher or lower number).

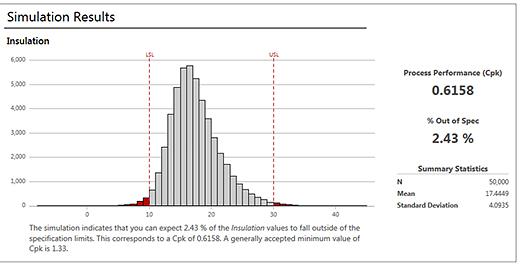Click here for larger image.

Companion interprets the results for you using output that is typical for capability analysis—a capability histogram, percentage of defects, and the Ppk statistic. It correctly points out that our Ppk is below the generally accepted minimum value.

Companion didn’t only run the simulation and then let you figure what to do next; it determined that the process is not satisfactory and presented a smart sequence of steps to improve the process capability.

It also knows that it is generally easier to control the mean than the variability. Therefore, the next step that Companion presents is Parameter Optimization, which finds the mean settings that minimize the number of defects while still accounting for input variability.

Click here for larger image.

Step 2: Define the objective and search range for parameter optimization

At this stage, we want Companion to find an optimal combination of mean input settings to minimize defects. You can use Parameter Optimization to specify your goal and use your process knowledge to define a reasonable search range for the input variables.

Click here for larger image.

Here are the simulation results:

Click here for larger image.

At a glance, we can tell that the percentage of defects is down. We can also see the optimal input settings in the table. However, our Ppk statistic is still below the generally accepted minimum value. Fortunately, Companion has a recommended next step to further improve the capability of our process.

Click here for larger image.

Step 3: Control the variability to perform a sensitivity analysis

So far, we’ve improved the process by optimizing the mean input settings. That reduced defects greatly, but we still have more to do in the Monte Carlo simulation. Now we need to reduce the variability in the process inputs to further reduce defects.

Reducing variability is typically more difficult. Consequently, you don’t want to waste resources controlling the standard deviation for inputs that won’t reduce the number defects. Fortunately, Companion includes an innovative graph that helps you identify the inputs where controlling the variability will produce the largest reductions in defects.

Click here for larger image.

In this graph, look for inputs with sloped lines because reducing these standard deviations can reduce the variability in the output. Conversely, you can ease tolerances for inputs with a flat line because they don’t affect the variability in the output.

In our graph, the slopes are fairly equal. Consequently, we’ll try reducing the standard deviations of several inputs. You’ll need to use process knowledge to identify realistic reductions. To change a setting, you can either click the points on the lines, or use the pull-down menu in the table.

Final Monte Carlo simulation results

Click here for larger image.

Success! We’ve reduced the number of defects in our process, and our Ppk statistic is 1.34, which is above the benchmark value. The assumptions table shows us the new settings and standard deviations for the process inputs that we should try. If we ran Parameter Optimization again, it would center the process, and we would likely have even fewer defects.

Plus, all this was done without collecting any further data because we know the typical distribution of the input values and have an equation that models the process.

How Can Monte Carlo simulation help you?

With Companion by Minitab, you can easily perform a Monte Carlo analysis to:
• Simulate product results while accounting for the variability in the inputs
• Optimize process settings
• Identify critical-to-quality factors
• Find a solution to reduce defects in processes