
Photo by Scott Graham on Unsplash
An engineer once told me, “I work on project teams that have an average half-life of two weeks, implementing solutions with an average half-life of two weeks.” Time after time, and in place after place, our improvement efforts often fall short of expectations and fade away. In this article, I will explain why this happens and what we can do about it.
|
ADVERTISEMENT |
Many improvement programs today are built around the use of experimental techniques. These techniques are proven ways of obtaining a lot of information in a short time. However, the problems keep recurring. To appreciate why this happens, we need to consider the relationship between experimental techniques and the types of problems we face.
Three types of problems
Myron Tribus (former dean of continuing engineering education at MIT) once described the problems we face as falling in the space defined by the three axes of Figure 1 (below). Tribus elaborates that we are taught how to handle problems as if they lie along only one axis or another, even though, in practice, our problems tend to involve either two or three axes at once.
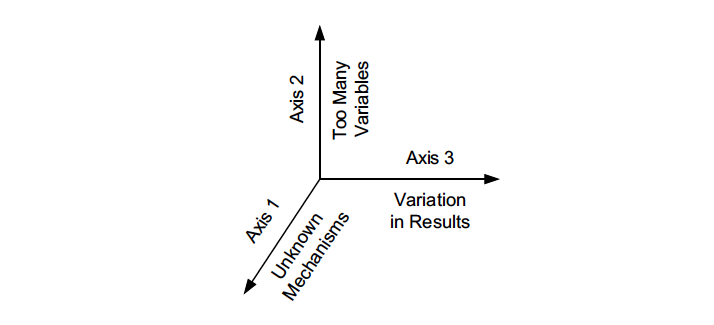
…
Comments
The Problem With Improvement Projects
Very interesting & helpful article. Thank you.
The Problem With Improvement Projects
So true Don.
Dr Ishikawa in his 1960's text on QC, explained his 3 Types of Cause Analysis:
a] So called Basic (4M's in those days)
b] Classification where these two are commonly called "Fishbone Diagrams" - even though Ishikawa recognised this but never described them as such); and
c] Process Classification Cause & Effect (Don Dewar RIP, QCI International, taught me in Reading Ca USA, his "Process Cause & Effect". Used in >80% of the time in Problem Solving projects.
Ishikawa’s text always explained, as you have and Myron Tribus too (heard him speak here in Australia as did Drs Deming and Juran), where the team votes for ranking based upon some evidence, for the Direct Cause (subject to then "5-Why analysis"; not on the Problem) and so called perceived Root Cause of the C&E diagram , it has too many variables in the inputs to the Event (aka "Fishbones") it is an unstable process (aka Process C&E).
In some ways the Automotive / Aerospace / Pharmaceutical use of the Process Control Plan, provides some discipline for selecting from the Process FMEA, the Key Control Characteristic and it along with a few but not many others, contribute to the Key Product Characteristics. These document some 'known' controls on the process variables and the risks from the PFMEA. Not all is known of course.
Of course, Process Behaviour Charts are powerful and understanding stability before capability, is essential as is having standards and standardizations with deviations/variations from such, enable better Problem Definition, and are integral.
I remember Dr Juran presenting in Sydney way back in 1990 at the AOQ Qualcon and subsequent workshops. Dr Juran acknowledged all the above and explained why he changed in his "Pareto Principle/80:20" of the "Trivial Many" to "Useful Many" of course keeping the "Vital Few". Dr Deming in his 1978 IQA/JUSE Tokyo paper agreed with Juran and called his ratio as "85:15".
If Ishikawa's Process Classification Cause Analysis was used more along with Control Charts and as you say, and Tribus, the variations and variables can be better understood, standardized and hopefully not repeat such.
The Process Control Plan and the precursor Process FMEA and its direct input of the Flow Process Charts (AIQG FMEA Text IV Ed), all completement such project team efforts. Thanks again Don. Nice to see you back.
Kudos to Don Wheeler
Thanks to Rod Morgan of Canada for re-posting this process improvement ‘gold’ from Don Wheeler. His work and that of Juran and Ishikawa before him is the basis of all Six Sigma, CI, 8D, DMAIC and Quality Control still taught today … by the good trainers.
Add new comment