When Sir Ronald Fisher created the analysis of variance (ANOVA) in the 1920s, he extended the two-sample t-test to allow the comparison of k sample averages. During the same time period, Dr. Walter Shewhart was creating the process behavior chart. So it should be no surprise that both techniques are built on the same mathematical foundation, even though they appear to be completely different at first glance. This column looks at the differences in what’s required to use each technique to improve a process.

A new product was being made on an existing production line that had no temperature control system for the bath. When the initial production run had 25% nonconforming product, the project team decided to see if they could improve things by controlling the bath temperature.

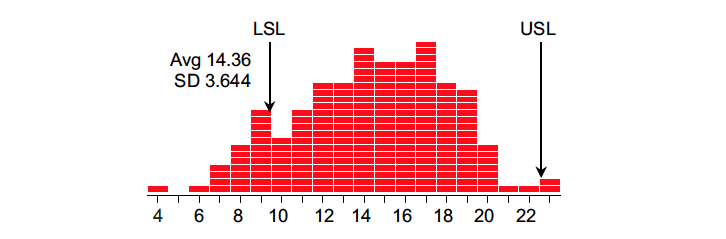
Figure 1: Process outcomes during experiment

A portable heat exchanger was brought in and used to control the bath temperature. The heat exchanger had four levels of operation: off, low, medium, and high. The process was allowed to run for an extended period of time at each setting to achieve thermal equilibrium. Audits were performed in the usual way until 50 values were obtained from each run. The 200 observations from these experimental runs are shown in Figure 1.

ANOVA

ANOVA seeks to determine whether the treatments studied in an experiment had a detectable effect upon the response variable. Here, the four levels for the heat exchanger define four treatments. So the first step in ANOVA is to organize the data rationally according to these four treatments. This results in the four histograms shown in Figure 2.

Figure 2: Histograms for treatments studied

The average of each histogram summarizes the effect of each treatment. The variation within each histogram shows the combined effects of all those factors that were neither studied nor held constant during the experiment.

While there is a trend in the four averages, the overlap between the histograms makes it unclear whether this trend is real. So do the treatment differences represent something real, or are they just random variation that could be due to the background noise?

Fisher chose to answer this question by comparing two different estimates of the variance of the original data. One estimate would be based on the differences between the treatment averages, while the other estimate would be based on the variation within the treatment histograms of Figure 2.

So, we begin by computing the standard deviation statistic using the four treatment averages.

The square of this statistic will estimate the variance for the treatment averages.

To convert this value into an estimate of the variance for the original data, we have to multiply by the number of original data in each treatment average,
n = 50.

The usual name for this estimate of the variance of the original data is the mean square between (MSB). Since it is based on k = 4 averages, it’s said to have
(k–1) = 3 degrees of freedom.

Our second estimate of the variance of the original data is found by squaring the standard deviation statistics for the four histograms in Figure 2 and  averaging the results. This estimate is known as the mean square within (MSW).

Since each term in the expression above has (n–1) = 49 degrees of freedom, the MSW is said to have k (n–1) = 4 (49) = 196 degrees of freedom.

When there are no detectable differences between the treatment averages, these two estimates of the variance will be estimates of the same thing and should be reasonably similar. But when the treatment averages differ, the MSB value will be inflated relative to the MSW value. So, Fisher compared these two estimates by dividing the MSB by the MSW. The result is known as the F-ratio.

When no signals are present, 99% of the F-ratios having 3 and 196 degrees of freedom will fall between zero and 3.88, as shown in Figure 3.

Figure 3: F-distribution and our observed F-ratio

Since our F-ratio of 7.15 is well outside the 99% coverage interval of zero to 3.88, we conclude that the treatments are detectably different, and we can interpret these differences as being real.

We return to Figure 2 to interpret the results. When the heat exchanger was “turned off,” they had an average near 13, and 12 out of 50 values were nonconforming (24%). When the heat exchanger was “on high,” they had an average near 16, the histogram was centered in the specifications, and there were only 6% nonconforming. This alone was sufficient to justify installing a heat exchanger for the bath.

After installing a permanent heat exchanger to control the bath temperature, further process audits resulted in the histogram shown in Figure 4. Now the average of 15.86 is near the midpoint of the specifications and the fraction nonconforming of 5.5% is consistent with the prediction from the project team. However, the standard deviation of the histogram in Figure 4 (3.46) is essentially the same as that in Figure 1 (3.64). While the project team had improved the process average, they did not reduce the process variation by any appreciable amount.

So while they were doing better, the process was still not operating within the specifications. And now the project team was out of ideas. All of the known cause-and-effect relationships had been investigated and no further ways to modify the process came to mind.

Figure 4. Histogram after heat exchanger installation

In order to use ANOVA to improve a process, the experimenter will need to identify the different treatments to be compared. ANOVA gives specific answers to the specific questions framed by an experiment, and it does this to the exclusion of all other questions. But what happens when you don’t know what questions to ask?

Process behavior charts

While ANOVA treats background noise as an obstacle to discovery, process behavior charts consider the background noise as an opportunity for discovery. They do this by examining the combined variation of all of the uncontrolled variables to see if it changes over time.

While ANOVA organizes the data into rational subgroups according to the treatment levels in the experiment, a process behavior chart uses data collected while no deliberate changes are made to the process. This allows us to organize the data into rational subgroups according to their time-order sequence. Instead of looking for the effects of a particular set of known treatments, a process behavior chart seeks to find evidence of changes in the process that indicate the presence of unknown variables that have large effects.

To this end, we want to choose our subgroups so they capture the routine process variation and nothing but the routine variation. This means that when we place two values in the same subgroup we are making a judgment that the two values were collected under essentially the same conditions. This need for homogeneity pushes us in the direction of small subgroups. Having many small subgroups also provides more opportunities for exceptional variation to show up between the subgroups. The need to use judgment to capture routine variation within the subgroups is why we talk about rational subgrouping as a foundation for effective process behavior charts.

When we have organized our data into some sort of rational subgroups, we once again use the variation within the subgroups to judge the variation between the subgroup averages. While the details of computation differ from those of ANOVA, the logic of the fundamental comparison remains the same.

For the 200 data of Figure 4, the order of production was used to create 40 subgroups of size n = 5. Next, an average and range was computed for each subgroup. The grand average of 15.855 characterized the location of the data. The average range of 4.625 summarized the routine, within-subgroup variation. This average range was converted into an estimate of the standard deviation for the original data by dividing by the bias correction factor for ranges of n = 5 data, which is d₂ = 2.326.

Next, this value is converted into an estimate of the standard deviation of the subgroup averages by dividing by root (n):

Rather than using a specific model to achieve some specified coverage, a process behavior chart uses generic, fixed-width, three-sigma limits because they have been thoroughly proven to filter out virtually all of the routine variation in every case.

If there is no exceptional variation present, these three-sigma limits will contain approximately 99% to 100% of the subgroup averages. If exceptional variation is present, we will expect to find some averages outside the three-sigma limits.

Figure 5: Average chart for Figure 4 data

Clearly, this process was going on walkabout. Some unknown causes were changing the process. As the production personnel plotted the process behavior chart in real time, they were able to identify these assignable causes of exceptional variation. As they took action to control these assignable causes, they were able to operate this process predictably and capably. The average chart and histogram for an additional 200 data are shown in Figure 6.

Figure 6: Histogram and average chart after controlling assignable causes

Now the process is operating on-target with minimum variance. It has an average of 16.12 and an estimated standard deviation of 1.78, which is half that of Figures 1 and 4. The capability ratio is 1.21 and the process is effectively producing 100% conforming product, so they no longer need 100% screening inspection.

Adding a heat exchanger to control the bath temperature improved things, but that was only part of the problem. By discovering the previously unknown assignable causes and removing their effects from the product stream, they completed the job begun by the project team.

The discovery of assignable causes will sometimes result in new technical knowledge, and sometimes it simply highlights dumb things that happen in production. Either way, they’re factors that stand out from the other uncontrolled variables and therefore contribute the lion’s share of the background variation. This is why their removal results in dramatically better production. Here, it cut the variation in half and eliminated the production of scrap.

Summary

While both ANOVA and process behavior charts compare the between-subgroup variation (our potential signals) with the within-subgroup variation (the probable noise), the differences in how the subgroups are formed tell of completely different objectives.

ANOVA seeks to determine whether the treatments studied have a detectable effect upon the response variable. As long as the project team can think of specific things to study, ANOVA will provide specific answers. However, in this quest for specific answers, the variation from factors outside the study will be lumped together and summarized by the mean square within. And in ANOVA, the MSW is the obstacle that our signals have to overcome.

Process behavior charts turn this around. Instead of manipulating some factors and ignoring the rest as background noise, they consider what happens when no deliberate changes are made in the process. (Incidentally, that makes them much easier to use in a production environment than experiments.) Using the time-order sequence, they examine the behavior of the combined variation of all of the uncontrolled factors. By allowing us to discover unknown process changes, they help us identify the assignable causes of exceptional variation behind these changes.

So here the combined variation of all the uncontrolled factors is no longer an obstacle to be overcome, but rather a mine of useful information to be exploited. Thus, a process behavior chart does not study a few factors that are deliberately changed, but studies all of the uncontrolled factors, both known and unknown, as they vary over time. Here, the objective is not to identify the effects of a specific factor but to see if any factors having a dominant effect remain unknown and uncontrolled. And it’s these dominant effects that make it worthwhile to identify and control assignable causes of exceptional variation.

What you don’t know can and will haunt you. Experiments will let you confirm what you think you know. But only process behavior charts help you to discover what you don’t know. They’ve been thoroughly proven. They work when nothing else will work. The only question is whether you will let them work for you.